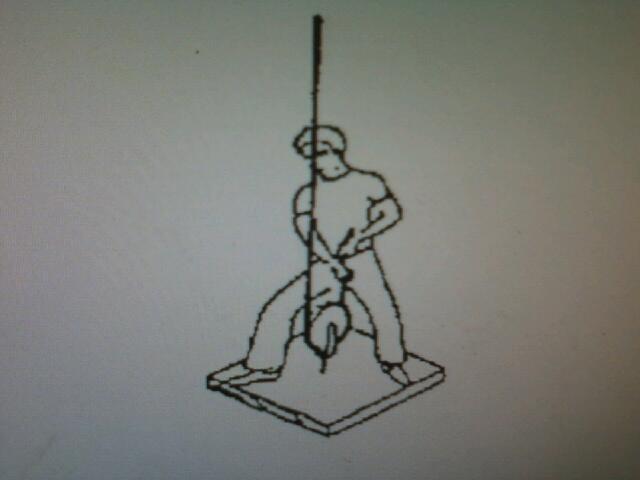
1. 그림과 같이 사람이 세팅을 하고,         

 2. 줄은 모든 힘을 버틸 수 있을 만큼 강하고,         

 3. 천장과 줄은 단단히 고정되어 있고,         

 4. 사람의 힘은 아주아주 세다.         

 5. 사람이 올라타고 있는 판은 땅위에 올려져 있고,         

 6. 줄을 당길때 중심은 흐트러지지 않는다.         

 이 사람은 판을 땅에서 띄울 수 있을까? 

정답은 : 올라 갈수도 있고, 못올라 갈수도 있습니다.

설명 들어갑니다.

우선 여기서 위로 올라가기 위해서는 ∑Fy의 방향이 +가 되야 합니다. (편의상 위쪽을 +로 하겠습니다.)

 첫번째로 우선 위에 탄사람이 +y방향으로만 힘을 작용하게 되면 사람이 필요한 힘 F는 [판의 무게(편의상 m1)+ 도르레의 무게(편의상 m2)+ 사람의 몸무게(편의상 m3)] * 9.8m/s^2  /2 가 필요합니다.(중력가속도를 9.8m/s^2라 할때)

다들 움직도르레다 아니다 말이 많은데 일단 움직 도르레 맞습니다.(줄 반대편이 사람이 가해지는 힘 F만큼으로 판을 들어올립니다. 즉 힘이 절반이 되는거죠.)

 하지만 여기서 뉴턴의 제3법칙에서 작용-반작용이 작용합니다. 어떤 힘을 가할때는 -방향으로 반대의 힘이 작용한다는 것이 작용 반작용의 정의이죠.

 여기서는 도르레에 작용하는 반대의 방향으로 다시 바닥(여기서는 판)에 반작용이 가해지는 거죠.

 즉 -F만큼 반대에 힘이 작용됩니다.

 따라서 ∑Fy는 사람의 몸무게 만큼(m3g) 아래로 작용되는 것입니다.

 이때는 힘의 합력이 지면쪽으로 향하고 있으므로 움직이지 못합니다.

 두번째로 사람이 y방향과 x방향으로(즉 비스듬히) 힘을 가할 경우를 생각해 봅니다.

 여기서 가정에보면 중심이 흐트러 지지 않는다고 했으므로(이조건을 판이 기울지 않는다고 생각한다면) ∑Fx=0이라고 생각하겠습니다.

 이렇게 되면 역시 위와 마찬가지로 사람이 y방향으로 주는 힘은 Fy = (m1+m2+m3)g/2*sinθ(θ값은 지면과 사람이 줄을 당기는 줄이 이루는 각도) 라 할수 있습니다.

 여기서도 ∑Fy=-m3g이므로 결국 움직이지 못합니다.

 세번째로 사람이 x방향으로만 힘을 가했다고 했을때 여기서는 사람이 가하는 힘 Fx가 Fy로 반뀌게 됩니다.

 즉 여기서는 ∑Fy=2Fx-m3g가 됩니다.

 여기서도 ∑Fx=0이라 생각하겠습니다. (조건 6에 따라.)

 여기서 사람가하는 Fx 방향의 힘이 m3g/2 이상이 되면 뜰수 있습니다.

 댓글 보니 작용반작용이 작용한다 않한다 말이 많은데요...

 모든 물체에 힘을 가하게 되면 반작용이 작용하게 되죠. 여기서 반작용은 사람이 판을 들어올리는 방향과 반대로(옆으로 기울던지 아니면 아에 x방향으로만 작용한다고 해도 반작용이 일어나게 되죠. 힘은 벡터이므로 -F가 작용하는 거죠) 작용하게 됩니다.

 우리가 물건을 들때 바닥에는 항상 반작용으로 힘이 작용합니다.

 쉽게 생각하면 모레에서 무거운 물건을 들면 발이 빠지는 것도 반작용 덕분이죠..

 자 여기서 실제로는 절대로 떠오르지 못합니다. 아니 떠오르긴 하지만 사람이 항상 쓰러지게 되있죠.

 Fx가 가해지게 되면 판은 결국 옆으로 기울어 지게 됩니다.(만약 중심이 흩드러 지지 않는게 사람만 중심이 흩드러 지지 않는다고 하고 판이 기울수 있게 되면 여기서는 판이 기울어져서 결국 사람이 떨어지게 되있습니다.)

 해답이 됬는지 모르겠네요.