학창시절 미술시간에 2차원인 도화지에 입체적인 도형을 그려보신적이 있을겁니다.

하지만 3차원의 도형을 2차원공간인 도화지에 그린다는것은 3차원도형의 어느 한부분에서 관찰한 부분을 그린다는 겁니다.

애니메이션 형식이 아닌 고정된 그림이 3차원 도형의 전부분을 한번에 나타내는 그림을 보신분은 없으실겁니다.

4차원의 도형은 아니 넘어서 n차원의 도형도 생각할수 있는데 (물론 3차원에 나타내기는 어렵습니다.)

우리가 도화지에 3차원 도형의 일부분을 그릴수있던것 처럼 4차원의 도형은 우리가 사는 이 공간 3차원에

일부분 (projection) 즉 사영하여 나타낼수 있습니다.

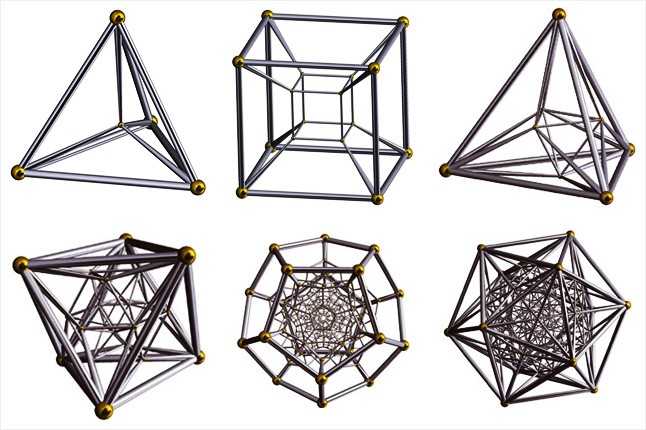
<출처: ? Robert Webb's Stella software

4차원 초 정다면체는 총 6개가 있습니다.

3차원 도형이 n개의 면을 가지면 n면체라고 하는 것 처럼 4차원 도형이 포함하고있는 입체의수가 n개이면

n-cell이라고 합니다. (3차원 도형이 2차원 도형인 면을 n개 가지는 것 처럼 4차원 도형은 3차원도형인 입체를 면으로 가짐)

n-cell을 애니메이션으로 보시죠

좌는 5-cell 우는 8-cell입니다.

물론 이는 4차원공간의 도형이며 5차원 6차원.. 쭉쭉해서 존재합니다.

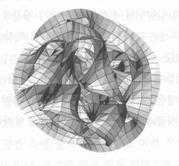
칼리비야우 공간이라는 10차원 시공간에서 도형은 이렇습니다.